Our recent work on entanglement of topologically ordered systems has been published in Phys. Rev. A

Unveiling topological order through multipartite entanglement Siddhartha Patra, Somnath Basu, Siddhartha Lalgapped liquids  entanglement  topological order  graph theory  
Dec 4, 2021  PRA 105, 052428 arXiv:2112.02253

It is well known that the topological entanglement entropy (\(S_{topo}\)) of a topologically ordered ground state in 2 spatial dimensions can be captured efficiently by measuring the tripartite quantum information (\(I^{3}\)) of a specific annular arrangement of three subsystems...

It is well known that the topological entanglement entropy (\(S_{topo}\)) of a topologically ordered ground state in 2 spatial dimensions can be captured efficiently by measuring the tripartite quantum information (\(I^{3}\)) of a specific annular arrangement of three subsystems. However, the nature of the general N-partite information (\(I^{N}\)) and quantum correlation of a topologically ordered ground state remains unknown. In this work, we study such \(I^N\) measure and its nontrivial dependence on the arrangement of \(N\) subsystems. For the collection of subsystems (CSS) forming a closed annular structure, the \(I^{N}\) measure (\(N\geq 3\)) is a topological invariant equal to the product of \(S_{topo}\) and the Euler characteristic of the CSS embedded on a planar manifold, \(|I^{N}|=χS_{topo}\). Importantly, we establish that \(I^{N}\) is robust against several deformations of the annular CSS, such as the addition of holes within individual subsystems and handles between nearest-neighbour subsystems. For a general CSS with multiple holes (\(n_{h}>1\)), we find that the sum of the distinct, multipartite informations measured on the annular CSS around those holes is given by the product of \(S_{topo}\), \(χ\) and \(n_{h}\), \(\sum^{n_{h}}_{μ_{i}=1}|I^{N_{μ_{i}}}_{μ_{i}}| = n_{h}χS_{topo}\). The \(N^{th}\) order irreducible quantum correlations for an annular CSS of \(N\) subsystems is also found to be bounded from above by \(|I^{N}|\), which shows the presence of correlations among subsystems arranged in the form of closed loops of all sizes. Our results offer important insight into the nature of the many-particle entanglement and correlations within a topologically ordered state of matter.

Show excerpt

Hide excerpt

---

Some background and questions addressed

This work is devoted towards understanding how topological entanglement entropy (TEE) of a topologically ordered ground state in 2 spatial dimensions can be detected via multi-particle information (MPI) and quantum correlation measures. It is well known that the von-Neumann entanglement entropy of a subsystem of a topologically ordered ground state obeys a modified area law, and contains a universal (i.e., geometry-independent) topological piece (dubbed as the topological entanglement entropy). Existing results also show that one can capture the topological entanglement entropy via a tripartite information measure for a particular arrangement of a collection of subsystems (CSS). The nontrivial tripartite information in turn reveals the existence of nonlocal 3-party correlations among the subsystems.

“In condensed matter physics, a string-net is an extended object whose collective behavior has been proposed as a physical mechanism for topological order by Levin and Wen. A particular string-net model may involve only closed loops or networks of oriented, labeled strings obeying branching rules given by some gauge group; others may involve still more general networks.” Caption source, Image source

This evokes the questions:

• Can there be entanglement beyond tripartite information and 3-party correlations within the topologically ordered ground state?
• If yes, how can we detect it?
• While the dependence of MPI on the topology of CSS has been hinted at in the literature, it has remained mysterious.

Answering these questions can lead towards a deeper understanding of the signature of many-particle entanglement and quantum correlations encoded within a topologically ordered ground state. Given that much activity is presently focused on the field of topological quantum computation, the questions raised above are fundamentally and technically important. Thus, obtaining some answers to these questions forms the primary objective of our work.

Main results: Topological invariance of multipartite entanglement

We begin our work by defining a general \(N-\)partite information in terms of von-Neumann entanglement entropies of various combinations of \(N\) subsystems. We show that for a topologically ordered ground state, MPI is independent of the geometry of the CSS. For a closed annular arrangement of the \(N\) subsystems in a CSS, the absolute value of MPI is independent of \(N\) and corresponds to a topological invariant, a product of the quantum dimension of the ground state manifold and the Euler characteristics of the graph corresponding to the CSS embedded on the planar manifold (\(\chi\)). We find that \(N-\)party irreducible correlations are bounded from above by the absolute value of this \(\)N-partite information. For the case of \(N=3\), the MPI formula reduces to the tripartite information capturing the TEE, and the 3-party irreducible correlations are found to be bounded from above by the tripartite information. Our findings thus agree with the already existing results in the literature, and further generalize to the case of an arbitrary \(N\).

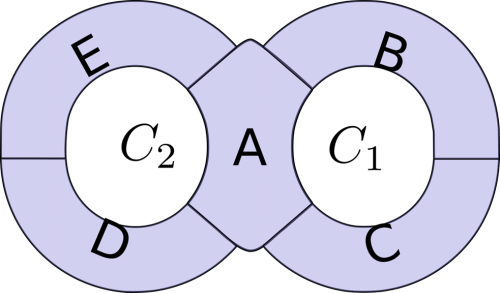CSS with five subsystems \((\left\{A_5(2)\right\} = \left\{A, B, C, D, E\right\})\) and embedded on planar manifold. The two holes in the CSS are denoted by C1 and C2.

Main results: Robustness of the topological nature

Apart from the simple closed annular structure of the CSS, we have studied various deformations of the CSS. The addition of holes/self-handles in the individual subsystems does not change the MPI measure. Similarly, the addition of handles between nearest- neighbour subsystems also leaves the \(N-\)partite information invariant. While the addition of handles between further neighbour subsystems trivializes the multipartite information measure for the entire system, one inevitably obtains several smaller closed annular CSS for which one can capture the same TEE once again. Further, the MPI measure gives a vanishing result for the CSS forming an open-chain structure. Our study, therefore, clearly demonstrates the importance of the annular arrangement of the subsystems in the CSS in capturing the TEE.

Main results: Nature of multipartite correlations

We have also studied a CSS with multiple holes, and shown that the sum of the absolute value of the multipartite information measured around each of the holes is again constrained by a product of topological invariants, e.g., the number of holes in the CSS (\(n_h\)), the Euler characteristics of the graph corresponding to the CSS embedded on the underlying planar manifold (\(\chi\)), and the quantum dimension of the ground state manifold. Further, for such topologically ordered ground states, we have shown that the \(N-\)partite information relation (for \(N>3\)) leads to an inequality relation, similar to the strong-subadditivity of von-Neumann entanglement entropies known for the case of three subsystems. This inequality shows the presence of non-zero \(N-\)party irreducible correlations (among the \(N\) subsystems arranged in a closed annular arrangement) that is upper bounded by the absolute of the \(N-\)partite information. This points to the presence of closed loop-like objects of all sizes being present in the topologically ordered state. Thus, our work offers several new results on the entanglement features of topologically ordered phases.

Our work shows the presence of correlations of all orders in the systems of particles.