Siddhartha Lal

Associate Professor, IISER Kolkata

Frustration shapes multi-channel Kondo physics: a star graph perspective Siddhartha Patra, Abhirup Mukherjee, Anirban Mukherjee, N. S. Vidhyadhiraja, A. Taraphder, Siddhartha LalKondo effect  impurity models  Kondo breakdown  non-Fermi liquid  
Jan 14, 2023  JPCM 35 315601 arXiv:2205.00790

We study the overscreened multi-channel Kondo (MCK) model using the recently developed unitary renormalization group (URG) technique...
We study the overscreened multi-channel Kondo (MCK) model using the recently developed unitary renormalization group (URG) technique. Our results display the importance of ground state degeneracy in explaining various important properties like the breakdown of screening and the presence of local non-Fermi liquids. The impurity susceptibility of the intermediate coupling fixed point Hamiltonian in the zero-bandwidth (or star graph) limit shows a power-law divergence at low temperature, signalling its critical nature. Despite the absence of inter-channel coupling in the MCK fixed point Hamiltonian, the study of mutual information between any two channels shows non-zero correlation between them. A spectral flow analysis of the star graph reveals that the degenerate ground state manifold possesses topological quantum numbers. The low energy effective Hamiltonian obtained upon adding a finite non-zero conduction bath dispersion to the star graph Hamiltonian for both the two and three-channel cases displays the presence of local non-Fermi liquids arising from inter-channel quantum fluctuations. Discontinuous behaviour is observed in several measures of ground state entanglement, signalling the underlying orthogonality catastrophe associated with the degenerate ground state manifold. We extend our results to underscreened and perfectly screened MCK models through duality arguments. A study of channel anisotropy under renormalisation flow reveals a series of quantum phase transitions due to the change in ground state degeneracy. Our work thus presents a template for the study of how a degenerate ground state manifold arising from symmetry and duality properties in a multichannel quantum impurity model can lead to novel multicritical phases at intermediate coupling.
Show excerpt
Hide excerpt

The physics of frustration

Frustration. We think we understand it, and how to deal with it. But what does frustration refer to in a quantum system? Consider classical spins (i.e., spins that have only two configurations, say, pointing up and pointing down) placed on a triangle and interacting with one another through a nearest neighbour antiferromagnetic Ising exchange interaction. It is easy to see that Néel (anti-parallel) ordering is no longer possible: for any two spins that are anti-aligned with one another, the third is left confused on which direction to choose. This confusion is labelled as the frustration of the classical Néel order.

An example of classical frustration: three spins on a triangle, connected by antiferromagnetic Ising interaction that favours antiparallel alignment. If the blue and green spins align in opposite directions, the third gray spin experiences conflicting interactions from the blue and green spins that want to align it downwards & upwards respectively.

Frustration can also been seen in quantum mechanical systems: while two quantum spin 1/2s with an antiferromagnetic Heisenberg interaction will form a maximally-entangled singlet state, introducing a third spin-1/2 creates a dilemma - the two-spin singlet cannot accommodate another spin (often curiously referred to as entanglement monogamy). Since the spin-flip quantum fluctuations of the system will want to lower the energy of the system by entangling all three spins, no spin can be left free and the two-spin singlet cannot be the true ground-state.

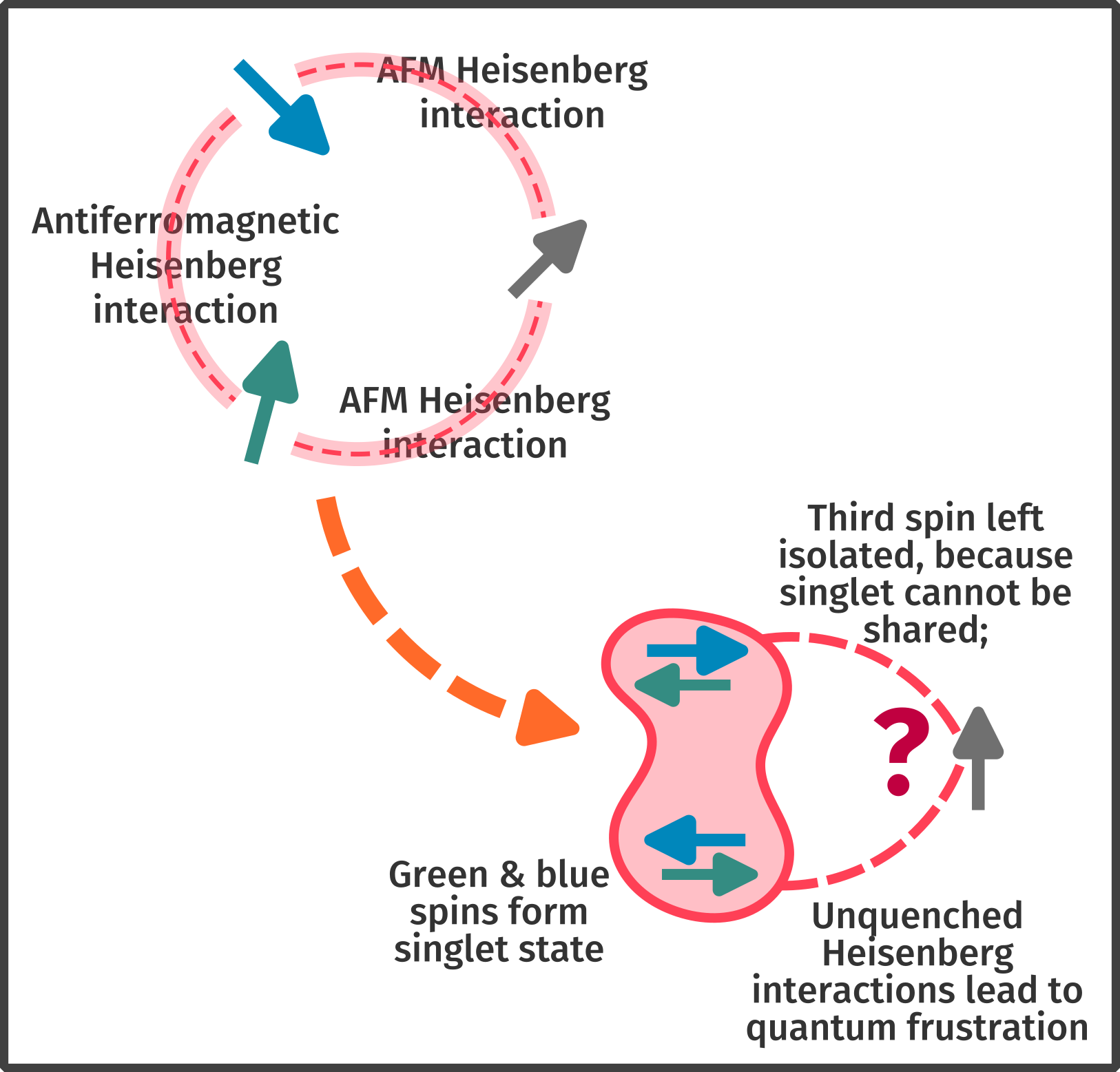An example of quantum frustration: three spins on a triangle connected by antiferromagnetic Heisenbeg interaction. The spin-flip fluctuations favour a singlet ground-state. However, if the blue and green spins form a maximally-entangled singlet state, they can no longer bind with the third gray spin (a property of the singlet), even though there are unquenched Heisenberg interactions between the third spin and the other spins respectively.

Frustration in the multichannel Kondo problem

The multichannel Kondo problem involves a local antiferromagnetic Heisenberg interaction between a single spin-1/2 impurity and the electrons of several conduction bath channels. Had there been only one conduction bath, the impurity moment would form a singlet together with a “cloud” of electrons from the bath. We refer to this as the screening of the impurity moment (as the singlet has no magnetisation). However, in the multichannel Kondo problem described above, the formation of a singlet between the impurity and electron from one of the conduction channels is frustrated. As a result, the so-called Kondo screening of the impurity spin’s magnetic moment is hampered.

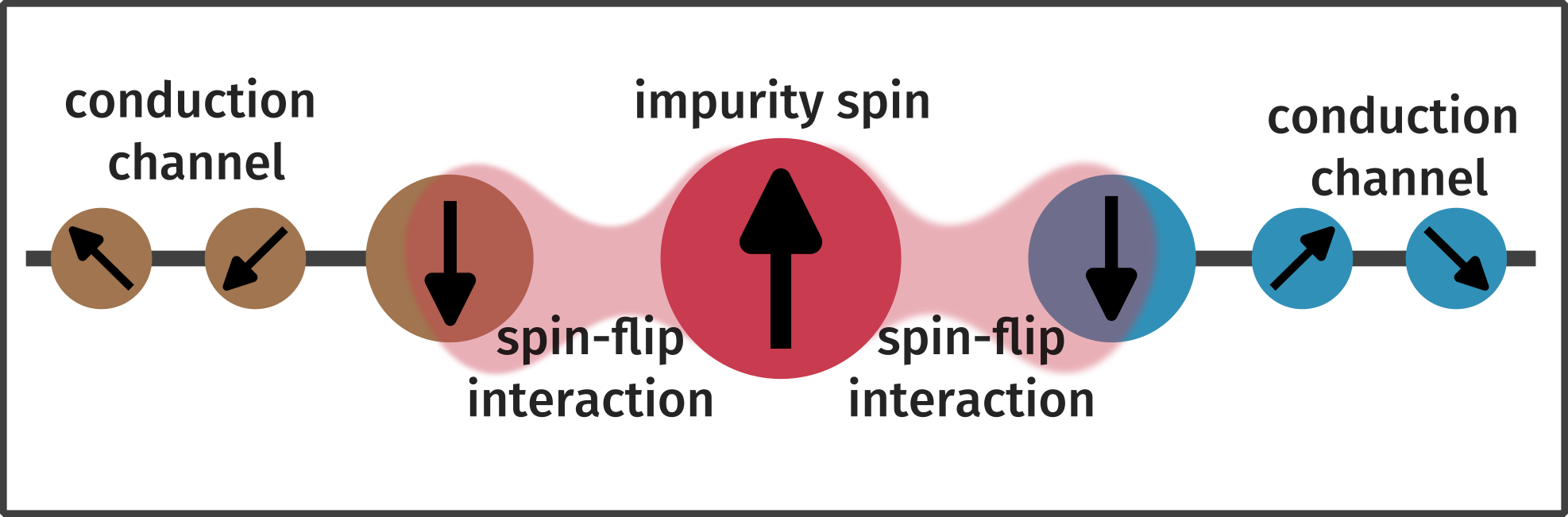Schematic of a multichannel Kondo model. The central impurity spin interacts with two conduction bath channels ( and ) through spin-flip interactions. The two channels compete with each other in trying to form a singlet with the single impurity spin, resulting in a novel frustrated ground-state.

Indeed, if the total spin of the conduction bath is greater than the spin of the impurity, the multichannel Kondo problem is said to be over-screened. The screening process, as well as its breakdown, are truly many-body in nature: a macroscopic number of conduction electrons interact with a single quantum impurity, and are therefore “aware” of each other. A proper description of the physics thus requires a field-theoretic treatment of the impurity-bath interactions, and the problem has been studied using a wide variety of powerful analytic and numerical methods.

Emergence of a “stargraph” in the multichannel Kondo problem

Our contribution in this work was to show that the fascinating properties of the N-channel Kondo problem could be linked to those of the associated skeletal problem: a central quantum spin-1/2 coupled to N quantum spin-1/2s (corresponding to the N conduction channels) through identical antiferromagnetic Heisenberg exchange couplings. Such a model is often referred to as a star graph, and it can be identified as a limit of the multichannel problem in which the kinetic energy of the itinerant electrons has been switched off.

A schematic of the stargraph model, the skeletal problem associated with any multichannel Kondo model. The graph consists of a central node (the impurity spin) connected with a number of outer nodes (the local spins of the conduction channels). The bonds connecting the nodes depict the Heisenberg interaction between the impurity spin and the conduction bath spins.

We show in our work that certain properties of the star graph, such as the ground-state degeneracy and the magnetisation, are linked to bulk thermodynamic properties. The star graph also sets the scattering phase shift of the conduction electrons, and the scattering phase shift then dictates how the quantum fluctuations resolve themselves in order to lead to novel features. In this way, the quantum frustration inherent in the underlying simple quantum mechanical problem is seen to offer great insights into a many-body problem which looks quite daunting otherwise. Please read our work to find out more.

Further details on our results (mostly for the experts)

  • We elucidate, within the context of the multichannel Kondo problem, the importance of the zero bandwidth limit of the RG fixed point Hamiltonian. We show that this zero bandwidth Hamiltonian directly leads to several properties of the MCK problem, like the ground-state magnetisation, scattering phase shift, Wilson loop and ‘t Hooft operators and degree of compensation.

  • The ground-state degeneracy of the zero bandwidth Hamiltonian is found to be topological in nature: the orthogonal states can be explored by the application of twist operators. Integrating out the impurity from the conduction bath states leads to the emergence of a topologically degenerate local Mott liquid.

  • We also demonstrate that the effective Hamiltonian for the gapless excitations of the fixed point Hamiltonian is of the non-Fermi liquid kind, involving scattering process that connect multiple conduction channels and leading to an orthogonality catastrophe in the ground-state. In momentum space, the self-energy resembles that of a marginal Fermi liquid localised near the impurity spin.

  • We link the non-Fermi liquid behaviour and orthogonality catastrophe with an “unrenormalised” scattering phase shift that can be obtained from the zero bandwidth problem; we show that this phase shift also leads to the well-known anomalous behaviour of quantities like the specific heat, magnetic susceptibility and thermal entropy.

  • Various entanglement measures, e.g., impurity entanglement entropy and impurity-bath mutual information, for the overscreened case show discontinuous behaviour as the conduction bath states beyond the zero-bandwidth problem are re-introduced via single-electron hopping. These discontinuities do not exist in the single-channel problem, and arise from the orthogonality catastrophe present in the overscreened ground-state.

  • By combining the strong-weak duality of the MCK Hamiltonian with that of the RG equations, we show that the strong-coupling theory is constrained to take a simple form. We also discuss an additional duality transformation connecting underscreened and overscreened models that involves exchanging the number of channels and impurity spin: this allows us to infer the infrared scaling behaviour of one class of models from a knowledge of the other.

You May Also Enjoy